por Susana Paz
Ciudad Universitaria. CDMX. 30 de mayo de 2022.- Anthony Torres Hernández, estudiante de doctorado en el posgrado de Ciencias Matemáticas adscrito a la Facultad de Ciencias (FC), publicó este mes un artículo en la revista Applied Mathematics and Computation de la editorial Elsevier en el que propone diferentes aplicaciones de una variante del cálculo fraccional, que busca unificar las diferentes definiciones de operadores fraccionales a través de la teoría de conjuntos.
Titulado Acceleration of the order of convergence of a family of fractional fixed-point methods and its implementation in the solution of a nonlinear algebraic system related to hybrid solar receivers, el artículo permite acceso libre de descarga gratuita durante un periodo de 35 días.
Se trata de la continuación de una propuesta que diseñó durante su tesis doctoral bajo la asesoría del doctor Fernando Brambila Paz, profesor de la FC, en la que propuso la creación de una nueva variante del cálculo fraccional que incorpora elementos de la teoría de conjuntos nombrada como cálculo fraccional de conjuntos, la cual se presentó por primera vez en el trabajo titulado Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods. Anthony Torres Hernández es egresado de la Licenciatura en Física de la Facultad de Ciencias y actualmente cursa el doctorado en el programa de Maestría y Doctorado en Ciencias Matemáticas y de la Especialización en Estadística Aplicada.
“En esta nueva publicación se reafirma que la propuesta de trabajar con conjuntos para caracterizar elementos del cálculo fraccional empieza a ser aceptada. La idea general es tratar de unificar las diferentes definiciones de operadores fraccionales a través de la teoría de conjuntos”.
El cálculo fraccional se puede considerar como una generalización del cálculo convencional, ya que las derivadas e integrales clásicas de orden entero pasan a ser definidas con respecto a un orden alfa real.
“Pero existe un problema en el cálculo fraccional y es que existen demasiadas definiciones de operadores fraccionales. Esto hace que la literatura que se puede encontrar sobre cálculo fraccional sea demasiado extensa y en algunas ocasiones repetitiva”.
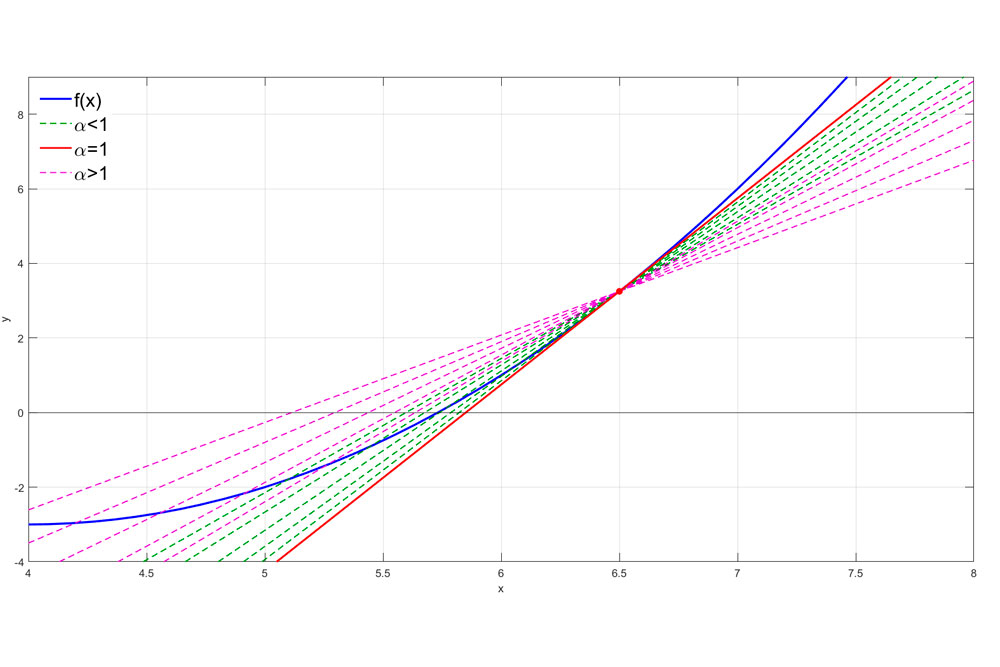
Esto lo llevó a la propuesta de unificar todos esos operadores fraccionales con la definición de un único operador perteneciente a una familia de conjuntos de operadores fraccionales, que se define al considerar una de las propiedades fundamentales del cálculo fraccional. Se trata de recuperar los resultados y definiciones del cálculo convencional cuando el parámetro alfa de los operadores fraccionales tiende a un entero positivo.
Hasta hace tiempo atrás, el cálculo fraccional parecía estar restringido a la matemática teórica, la propuesta de Anthony Torres pretende generar diferentes aplicaciones de los operadores fraccionales que abarquen tanto la matemática teórica como la matemática aplicada.
“Lo novedoso de este trabajo es que permite que cualquier persona que no esté familiarizada con la teoría del cálculo fraccional pueda entrar y generar aplicaciones analíticas a través de la teoría de conjuntos y, al profundizar más, generar aplicaciones concretas relacionadas con física e ingeniería”.
Para Anthony Torres, el que se estén generando una gran cantidad de artículos en el que solo se presentan nuevas definiciones de operadores fraccionales, genera una saturación de artículos en la que se estudia un mismo modelo con la única diferencia del operador implementado.
“Identificamos esto como un problema y propusimos usar un único operador que a través de ciertos conjuntos permitiera unificar las diferentes definiciones de operadores fraccionales”.
Una de las aportaciones más importantes —afirma el estudiante— es la incorporación de la teoría de grupos al cálculo fraccional. El trabajar con conjuntos le permitió definir grupos de operadores fraccionales isomorfos al grupo de los enteros bajo la suma, así como subgrupos cíclicos de operadores fraccionales.
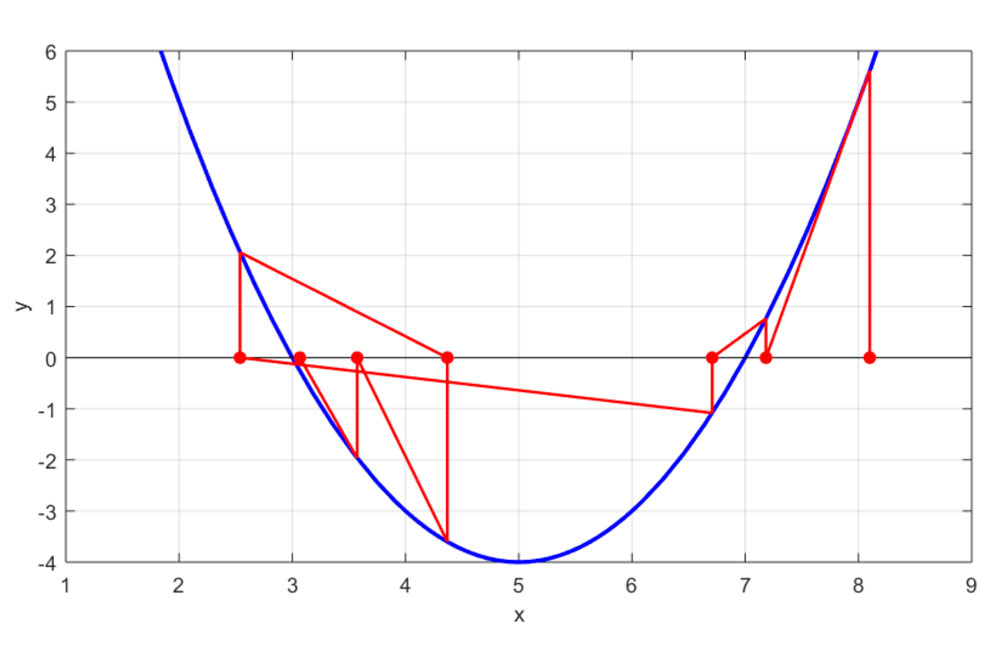
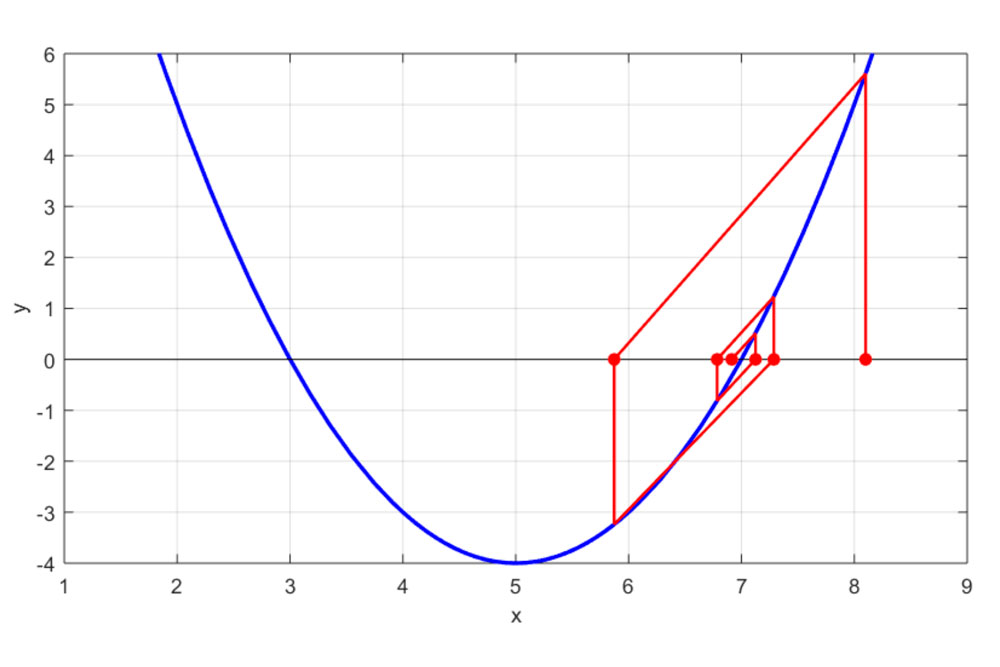
El segundo punto es que el uso de conjuntos de operadores fraccionales permite clasificar propiedades de manera general. En el artículo se muestra como clasificar a través de conjuntos el orden de convergencia de familias no numerales de métodos de punto fijo.
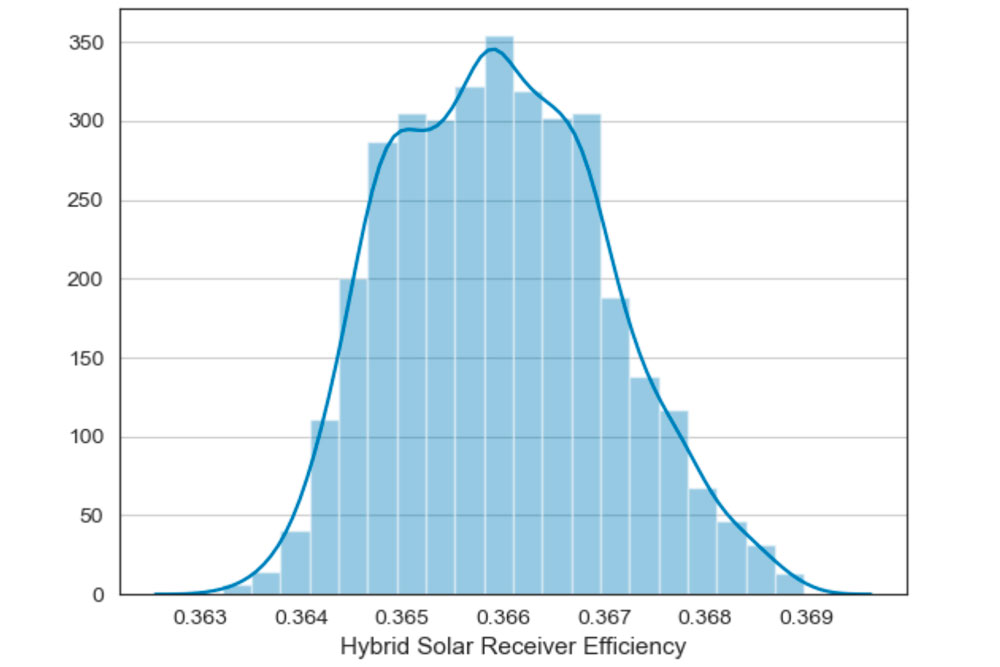
Una tercera es que permite la resolución de un sistema de ecuaciones no lineal relacionado con el análisis de las temperaturas y eficiencias de paneles solares híbridos, mediante el uso de métodos de puntos fijo que utilizan operadores fraccionales, mostrando su utilidad en un problema real.
El último punto es permitir generar un cálculo fraccional de variable compleja siguiendo la lógica de lo que se muestra en el artículo. Por lo que permite, de manera sencilla, que se puedan generar métodos de punto fijo fraccionales de variable compleja y al mismo tiempo clasificar su orden de convergencia.
Para Anthony Torres esta publicación representa un logro con el que culmina su quinto semestre de doctorado en el que, a partir de la asesoría y el apoyo del doctor Fernando Brambila y de la Mat. Beatriz Britto, le permitió internarse en este tema que le parece tan apasionante.
El estudiante expresó que los resultados expuestos no habrían sido desarrollados sin el apoyo incondicional de su familia cercana, en especial de su abuela Alicia y su hermana Wendy, así como de su tía Roxana y sus primos Barbara, Humberto y Yoel.
También manifestó que sus estudios de doctorado no habrían sido posibles sin aquellas personas que lo ayudaron, de forma directa o indirecta, en la etapa final de sus estudios en la Licenciatura en Física de la FC, entre las que se encuentran el doctor Miguel Bastarrachea, la M. en A. Reyna Caballero, la doctora Mirna Villavicencio y el doctor Alberto Güijosa. Así como de las personas que lo ayudaron, de forma directa o indirecta, al inicio de sus estudios en la Maestría en Ciencias Matemáticas de la UNAM, entre las que se encuentran el doctor Fernando Brambila, la Mat. Beatriz Brito, la doctora Silvia Ruíz-Velasco y la doctora Úrsula Iturrarán. Por último, pero no menos importante, expresó su agradecimiento a todas aquellas personas que le brindaron su apoyo desde el inicio de sus estudios en la Licenciatura en Física hasta el momento actual de sus estudios de Doctorado en Matemáticas, entre las que se encuentran la M. en C. Paulina Colín.
Aquí puedes consultar los artículos:
Acceleration of the order of convergence of a family of fractional fixed-point methods and its implementation in the solution of a nonlinear algebraic system related to hybrid solar receivers
https://authors.elsevier.com/a/1f55HLvMgV1Xo
Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods
https://doi.org/10.3390/fractalfract5040240